Last year, as the impact of one tiny virus rippled across the entire world and upended virtually every facet of human civilization, Los Alamos scientists discovered that quantum-level disruptions, rippling across time, do not spiral out of control. According to the scientists’ simulations, one can take a particle in a specific quantum state back in time and deliberately modify its state in the past without significantly changing it in the present. Voilà: the butterfly effect—in which tiny changes progress into enormous ones—is thwarted at the quantum level.
“It’s a little more complicated than that,” groans Los Alamos physicist Bin Yan. “For starters,” he says, “there’s more than one way to construe the butterfly effect.”
Indeed there is. Sixty years ago, MIT Professor Edward Lorenz was running a weather simulation and rounded off one of the parameters from six decimal places to three. To his surprise, two months of simulated weather were completely different as a result. He would later liken the situation to the flap of a butterfly’s wings spawning a distant tornado. That’s the butterfly effect most often mentioned; it’s an expression of chaotic behavior. In complex systems such as the weather, a small change in the conditions at one moment can produce an enormous subsequent change overall.

But an earlier version of the butterfly effect derives from the 1955 short story A Sound of Thunder by Ray Bradbury. In it (spoiler alert), a man time-travels back to dinosaur times and accidentally steps on a butterfly. When he returns to the present, everything has changed: people’s attitudes are different, words are misspelled, and a different candidate has won the recent presidential election.
Yan’s point is this: the two butterfly effects are related but differ somewhat in character. Lorenz tells a story of chaotic behavior, of small causes producing big effects due to the complexity of the system. Such things can evolve fairly quickly. (Indeed, some scientists argue that accurately predicting the weather more than two or three weeks out will always be impossible, for precisely this reason.) Bradbury tells a story that’s more timeline sensitivity than chaos—small changes being amplified in modest increments over the long haul, like biological evolution—and, technically, involves a backwards-in-time operation.
Ever the overachiever, Yan worked out the quantum analogues of both.
Quantum chaos
“At the outset, it wasn’t clear that quantum chaos would even exist,” says Yan. “The equations of quantum physics give no immediate indication of it.”
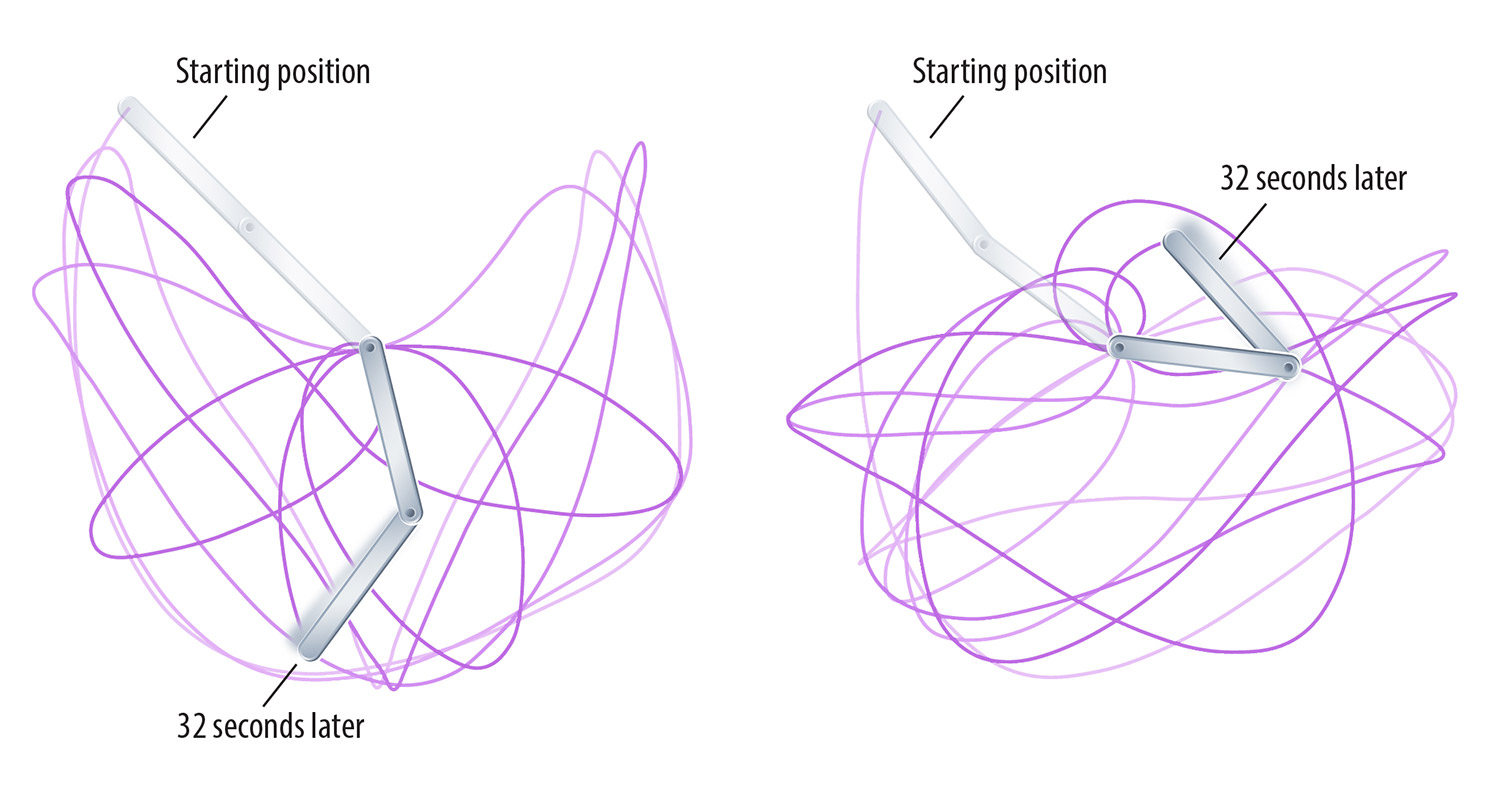
In classical (nonquantum) physics, objects can be treated as a collection of point particles in distinct locations with distinct states of motion. Yet despite such a rigid description of reality, there are times when chaotic behavior readily emerges. Even a small number of simple objects can be assembled in such a way that small changes in the initial setup lead to wildly varying outcomes. A common example is a frictionless pendulum made from two equal-length rods joined by a hinge, similar to a human arm (although in the case of the pendulum, its “elbow” may freely hyperextend). Where a single-rod pendulum released from a horizontal position would swing back and forth repeatedly along the same semicircular arc, a double-rod pendulum would flail about in an enormously complicated fashion, folding and unfolding as it swings and sometimes windmilling its lower arm full-circle around its elbow. If it were released from a slightly different height or with its elbow ever-so-slightly bent one way or the other, the sequence of motion would be entirely different.
At the outset, it wasn’t clear that quantum chaos would even exist.
But unlike classical physics, the quantum description of reality does not specify discrete objects at distinct locations with exact states of motion. The basic “object” is not generally a solid entity but rather a diffuse type of particle imbued with certain wave properties. The mathematical description of its state is called a wave function, and according to the equation governing wave functions, a particle in a fixed energy state doesn’t change in time. The more general case of numerous particles in a mixture of states makes the math considerably messier, but a key feature remains: because the equation governing the time evolution is linear, small changes in the initial configuration remain small as time passes. There is no obvious provision for the emergence of chaotic behavior.
Studying chaotic behavior in the quantum realm, therefore, has often involved a little cheating. A pristine quantum system (intended to be analogous to something like a frictionless double-rod pendulum, perhaps) is not chaotic on its own, in the sense that a change in initial conditions doesn’t generate complex outcomes. But it might become chaotic if one accounts for a non-pristine system. In particular, by acknowledging that a quantum object, such as an atom, can never be fully shielded from its environment—there are always at least a few stray radio waves or magnetic fields or whatnot flitting about, even in the most tightly controlled laboratory—one can introduce some realistic variations into the equation and thereby obtain complex results. About 20 years ago, scientists defined a quantity known as a “Loschmidt echo” to capture the degree to which variations in a system’s environment allow for the emergence of such complexity.
The connection among measures of quantum chaos was suggestive. We were closing in on something.
But is that really the same thing as chaos? Is it the Lorenz-type butterfly effect?
“In those early studies,” Yan explains, “environmental perturbations, and the Loschmidt echoes that quantify their effect, were viewed as a necessary substitute for true chaos. But it was unclear if there was a genuine butterfly effect at work. After all, we weren’t taking some tightly controlled system and perturbing its initial conditions; we were perturbing its exposure to the outside world.” Even a boring, back-and-forth, single-rod pendulum might exhibit complex behavior if it were being batted around by wind and hail.
Baby butterflies
As the 21st century progressed, quantum chaos researchers continued to use Loschmidt echoes and other comparable measures to characterize, well, whatever it was that wasn’t exactly chaos but wasn’t exactly not either. The relationship to Lorenz-type butterflies remained uncertain. Then in 2015 another quantity gained a great deal of attention within the research community: the out-of-time-order correlator, or OTOC. It examines any two measurable properties of a quantum system (its energy and its rotation, perhaps), but it does so in a scrambled time order. Specifically, it considers measuring one property in the present, then mathematically allowing the system to evolve backward in time and measuring the other property in the past, and subsequently returning to the present to assess how different the first property is. Now, quantum measurements normally disturb whatever they’re measuring, so if you measure this and then that and then remeasure this again, even without all the bother of time travel, you generally get a different result the second time. But the OTOC captures a key variation on that effect by including forward and backward evolution in time. Essentially, the OTOC is a measure of the Bradbury-type butterfly effect.
Yan decided to see if he could find a bridge between the two key quantities in the emerging field of quantum chaos, the Loschmidt echo and the OTOC. He and his Los Alamos colleagues Lukasz Cincio and Wojciech Zurek—(Cincio recently won the IBM Quantum Challenge, while Zurek is widely recognized for foundational research bridging the quantum-classical divide with a theory of quantum decoherence)—set out to see if they could link the two analytically (pencil and paper) or numerically (via computer calculation). As it turned out, they could do both: they found that the two were intrinsically related, that the OTOC could be approximated from the Loshmidt echo. Complex quantum systems, it seemed, had elements of both butterfly effects.
“The connection between OTOC and Loschmidt echo—between Bradbury and sort-of Lorenz—was suggestive,” says Yan. “We were closing in on something. And yet, all along, there was a nagging sense that something was unsubstantiated, that we were getting ahead of ourselves.” Yan notes that a classical chaotic system, like a double-rod pendulum, still has an exact position and state of motion at any moment, while a quantum wave function generally has neither. “It was never entirely clear that wave functions were suitable quantities for exploring of quantum chaos.”
Working this time with a colleague from Caltech, Yan set out to see if he could learn anything by trying to justify the use of wave functions in chaos studies. Borrowing a concept called “circuit complexity” from quantum computing, he analyzed the relative complexity of quantum wave functions in order to precisely quantify how much two initially similar wave functions will deviate from one another over time. This is the essence of chaotic behavior, slight variations in initial conditions leading to large, system-wide departures, and by this circuit-complexity measure—unlike the standard measures of wave-function overlap used in quantum mechanics that stay constant during the time evolution—the wave functions did indeed diverge with time. It even turned out that the complexity growth separating initially similar wave functions could be calculated with OTOCs.
At the quantum scale, reality is self-healing.
The circuit-complexity approach clearly worked, and its connection to the OTOC was encouraging, but was it actually correct? To verify this, Yan performed a key consistency check in physics, examining whether his new approach would successfully reproduce known results in a situation that had already been solved. For example, Einstein’s gravity theory, which properly governs extreme gravitational situations, such as a black hole or the big bang, reduces to Newton’s much earlier gravity theory in less extreme situations, such as the orbit of the moon or the trajectory of a baseball. Yan was able to show that the circuit-complexity approach to quantum chaos properly reduces to the standard measure of classical chaos under appropriate conditions.
So here, at long last, was the Lorenz-type quantum butterfly effect. A quantum wing flap could theoretically produce a quantum tornado. And while a lesser scientist might have just declared victory, Yan felt there was something special about the way the OTOC, a Bradbury-type butterfly, naturally shows up in Lorenz-type quantum chaos. The interrelation implied fertile ground for exploration—and perhaps a hidden reality yet to be revealed.
The anti-butterfly effect
Yan and his Los Alamos colleague Nikolai Sinitsyn set up an experiment to test the quantum butterfly effect, Bradbury-style, on an IBM-Q quantum processor.
A regular, nonquantum computer performs calculations by taking a bunch of bits of information, ones and zeros, and sending them through a complicated “logic circuit,” the elements of which are called gates. Along the way, the ones and zeros interact with one another. (For example, the AND gate compares two bits and returns a value of 1 only if both bits were already 1; if either was 0 to begin with, the gate returns 0.) A quantum computer does its calculations the same way, except that it uses quantum bits, or qubits, and has some additional gates that only work with qubits.
Qubits differ from classical bits in two important ways. First, they carry more complicated information than a binary one or zero. Second, when they interact with one another as they are passed along a logic circuit, they become “entangled,” meaning that they cease to be purely individual qubits and instead share their states. Probing one member of an entangled group of qubits—for example, checking its value—will in some way affect the state of all the others.
Yan and Sinitsyn created a complicated logic circuit and prepared a group of qubits to send through it. However, for this experiment, they sent the qubits through the circuit in reverse order—the last gate first, the first gate last—to simulate the qubits’ states evolving backward in time. Once the qubits had passed backward through the circuit, becoming entangled along the way, the scientists measured the state of one qubit. Because measurements in quantum physics affect the object being measured in an unpredictable way, this measurement amounts to deliberately damaging the state of that qubit and therefore the information it carries. In addition, all of the other qubits entangled with it would also be partially modified.
But here’s the trick: now, Yan and Sinitsyn send the qubits, including the directly damaged one, forward in time—i.e., passing through the circuit of logic gates again, but this time in the proper forward direction. To their great surprise, the scientists found that the damaged qubit, once returned to the present, was actually in its original state (the “before time travel” state), modified only by some small background noise. The same was true of all the other qubits. As long as the circuit is complicated enough to produce significant entanglement among the qubits, the potential damage is curtailed; any information damaged in the past is recovered in the present.
“It’s effectively the opposite of the Bradbury-type butterfly effect!” says Yan. “At the quantum scale, reality is self-healing. Entanglement is preserving the present, protecting it.”
Better living without butterflies
Successfully exploring the nature of the quantum butterfly effect—via either perspective, Lorenz or Bradbury—would have been prize enough. But Yan and his colleagues got an extra bonus with the discovery that natural entanglement serves to restore damaged information. And this quantum anti-butterfly effect—now that it is known to exist—can be put to use.
Entangled qubits might be exploited to provide a reliable rescue against information loss.
The most obvious application is a straightforward assessment of “how quantum” a quantum computation is. To what extent is a quantum computer actually making use of its quantum resources, rather than relying on its classical ones? “In principle, finding the answer is simple,” says Yan. “Create a forward-and-backward logic circuit to check for the preservation of information. Since the anti-butterfly effect is a purely quantum phenomenon, the degree to which information is protected represents the degree to which it is quantum information to begin with.”
More ambitious, perhaps, would be a direct information-security application. In principle, any information can be encoded in qubits and protected from damage with a forward-and-backward logic-circuit operation. Whether the threat of damage comes from a prosaic vulnerability—such as a power surge, a computer glitch, or ever-present natural radioactivity affecting physical circuitry—or from a deliberate cyber attack, the anti-butterfly nature of entangled qubits might be exploited to provide a reliable rescue.
And of course, there’s the most important application of all: when we finally do learn to send people back in time, maybe we can construct a suitable quantum anti-butterfly gizmo to prevent time-travel tourists from disturbing the timeline we’ve all come to know. LDRD