Great strides have been made in the last few decades to shed light on the fundamental electronic structures of actinide complexes and materials. First-principles calculations, including density functional theory (DFT) and wavefunction-based methods, have been instrumental in predicting structures, elucidating the role of d-and f-orbitals in bonding, and in extracting electronic structure information from the complex spectroscopic data of actinide materials and molecular systems.
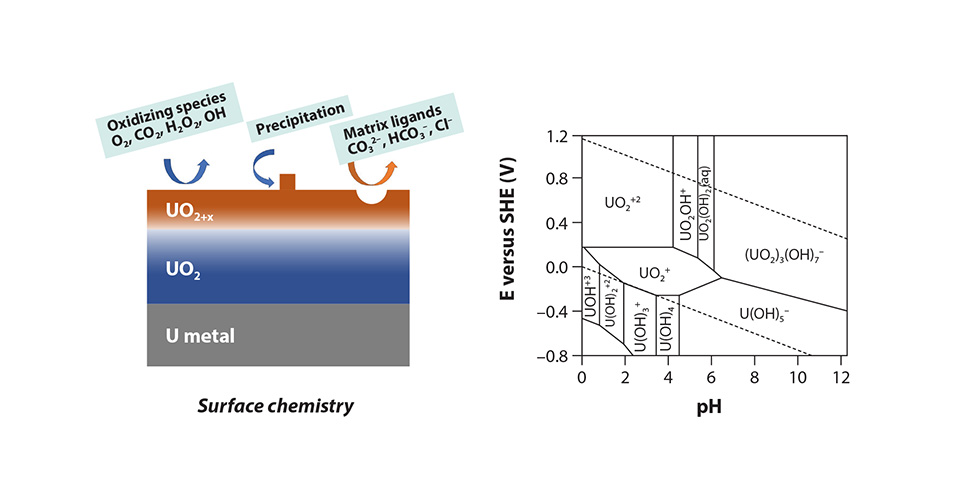
While great advances have been made in the fundamental understanding of actinide complexes and materials through first-principles calculations, the field continues to evolve with a growing need for new approaches to give faster and more chemically realistic dynamical simulations, beyond static calculations. Some of the challenges include understanding the chemical coordination environment of actinides and lanthanides in solution, mass transport in actinide/lanthanide separation processes, surface reaction mechanisms, electrochemistry, and phase transitions in actinide materials and their mechanism as a function of temperature and pressure. Fig. 1 highlights two complex examples of surface and solution chemistry of uranium for which we have limited understanding at the molecular level. The dynamic simulations are essential for a deeper understanding of these complicated processes in actinide science, however, they also bring new challenges, particularly in developing an accurate description of the diverse and dynamic nature of redox-active actinides. In this article, we present a brief overview of the current methodologies for simulating dynamic actinide systems and offer our perspective on the future directions in which this field could beneficially evolve.
Molecular dynamics
Molecular dynamics (MD) simulation is an extremely powerful technique because it gives a realistic picture and sampling of the atomic conformation space. Besides being a phase space sampling technique, yielding coordinates and momenta, this technique allows for the study of time-dependent phenomena such as diffusivities, solubilities, ligand residence times, and ligand exchange dynamics. MD simulations have been a crucial tool to address dynamic effects in many research areas, for example in materials science and biological systems, leading to groundbreaking discoveries.
Conceptually, molecular dynamics is very intuitive. Given the potential energy of a system, typically as a function of the positions of all the nuclei, the forces on each atom are calculated. Setting initial conditions with the atomic coordinates and velocities, the equations of motion are numerically integrated in discrete steps of time, giving the trajectory of all the atoms in the system. Techniques for integrating
the equations of motion in different thermodynamic ensembles were developed more than 70 years ago and algorithms for evolving the trajectories are in a highly optimized state, allowing for large-scale simulations. When using molecular dynamics to study actinide sciences, additional complexities stem from the redox sensitivity inherent to most actinide systems. Multiple oxidation states can coexist or change during the reaction process, requiring a description of the change in oxidation states for the same element in one simulation cell. In these situations, elements of the quantum-level theory should remain, in spite of the approximations, to capture events such as charge transfer and redistribution processes dynamically.
Depending on the level of theory at which the potential energy surfaces are calculated, the simulations can be largely divided into three categories: first-principles MD, semi-empirical MD, and classical MD, with increasing levels of approximation. All three levels have their pros and cons, going from more accurate and portable yet very computationally time consuming, to computationally fast at the expense of introducing approximations.
A range of approximations exist in the literature and here we remark on two approaches: the development of empirical functions—simple functions of the nuclear positions—and semi-empirical formulations which preserve the electronic degrees of freedom that are removed in the empirical approach, albeit with parameterized dependence. Both have their advantages and disadvantages, stemming from the simplifications incurred. Empirical methods gain speed at the expense of removing electrons from the system, whereas the semiempirical methods retain the electronic effects however at higher computational cost.
Quantum mechanical potential energy surfaces
The most accurate methods to compute potential energy surfaces are quantum-mechanics-based. Whereas solving Schrödinger’s equation for more than a handful of atoms is unfeasible, DFT provides a reasonable alternative. To obtain the forces on the atoms requires computing the molecular orbitals for all the electrons in the system and then using these electronic states to calculate the energy gradient as a function of the nuclear positions. Currently, the two most widely used methods in this domain are the DFT-based Car-Parrinello Molecular Dynamics (CPMD) and Born-Oppenheimer Molecular Dynamics.
Electronic structure methods are very attractive because they are completely transferable (do not depend on what molecule one is studying) and the charge state of the atoms naturally arises from the simulation. Hence, first-principles MD simulations have been successfully applied to various systems to provide atomic pictures, such as molten salts and fast chemical reactions which can reach equilibrium at short timescales.
While accurate, these simulations are computationally demanding and very difficult to scale to take advantage of high-performance computers. Currently, modern methods that can accurately simulate systems containing heavy elements are limited to roughly 200 atoms (Fig. 2), taking on the order of three minutes for one calculation of the atomic forces, limiting its applicability to very short MD trajectories (picoseconds) with wall-clock simulation times reaching weeks. To achieve a reasonable sampling, trajectories on the order of hundreds of picoseconds are needed, involving approximately 200,000 calculations of the forces (taking over 400 days!). The short timescale may not provide sufficient statistical information, leaving critical questions unanswered, particularly in areas such as surface corrosion processes, which involve phenomena such as oxygen migration that often occur at nanosecond timescales or longer.
Furthermore, the time-per-force computation scales with the cube of the number of atoms in the system, or O(N3), therefore, trajectories incorporating thousands of atoms are unfeasible with this level of theory. While these approaches provide valuable insights into short-range interactions, they present challenges in fully capturing the complexities of actinide systems. For example, the limited length scale in these simulations often fails to adequately represent the second or third coordination shells.
The key computational expense is the calculation of the total energy of the system and its derivatives, i.e., the forces on each atom. Therefore, the time to compute the forces is pivotal in the usefulness of the MD technique. To address these shortcomings that derive from the high computational demand of the first-principles methods, approximated forms of the energy function have been developed.

Figure 2. Various methods for molecular dynamics simulations and their time-length scales.
Empirical potential energy surfaces
The key ingredient for an MD simulation is the potential energy function U(R); the quality of the simulation will only be as good as the accuracy of this function. The large-scale MD simulations found in the literature are based on empirical interatomic potentials, i.e., functions of the inter-nuclei positions, rij. These functions are developed empirically and fitted to physical properties (e.g., diatomic dissociation curves, samplings of potential energy surfaces by massive ab initio calculations, radial distribution functions, etc.). These empirical potentials combined with the latest algorithmic developments of computation and parallelization are very fast. Simulations of, for example, shocks through materials can be performed with millions of atoms for extended timescales to visualize reorganization of materials and defect formation. These large simulations most often involve light elements in systems such as explosives or biological matter, where the interatomic interactions are simpler than those among f-elements, and mature potentials have been developed.
The development of accurate empirical potentials for the actinides can be surprisingly difficult because a single function of rij needs to be derived that accurately mimics the radial, angular, and polarization nature of all the electrons combined. One approach taken in the past to tackle these difficulties has been to consider whole molecular units, such as UO22+, H2O, etc. However, for example, if the pH of the solution were to change, requiring H2O dissociation into OH– and H+, this would call for further development of the model. Capturing changes in oxidation state with these approaches is difficult, although techniques have been developed that introduce charge as a dynamical variable and electronegativities as parameters, although this approach has not been used for simulating actinides, as far as we are aware. On the other hand, situations such as ion migration and coordination present more benign modeling conditions and lend themselves to study via empirical potentials, with all the advantages of computational speed that this confers. To make the development of empirical potentials for actinides approachable, research groups have explored a few methods such as simulating the interaction of the late actinides as spherical units via 12-6-4 Lennard-Jones type functions or reducing the complicated electronic structure of the actinide ion by folding it into simulations of the UO22+ ion as a unit., More sophisticated polarizable force fields have been developed for some actinide ions and applied to simulate liquid-liquid separation.
In the last five years, the field of machine learning (ML) has been making inroads into the parameterization, or training, of interatomic potential energy functions. Success has been reported for light elements but the application of these approaches to the f-elements is in its infancy. The ML universal potential M3Gnet has been trained throughout the periodic table, including the actinides. These potentials show great promise for their speed and we expect to see them becoming very useful in the foreseeable future.
In the chemical reactions of actinide and lanthanide systems, it is imperative to include a description of charge transfer and chemical bond dissociation/formation for accuracy and interpretability. To capture effects that are purely electronic in nature, methodologies are needed that explicitly include the electronic degrees of freedom, even if in parameterized form. The first-order approximation of such approaches comes from the self-consistent-charge (SCC) methods which we discuss next.
Semi-empirical methodologies
A middle road between first-principles and empirical methods is a family of semi-empirical methodologies that preserve the electronic degrees of freedom that were removed in the empirical potentials described above. They reduce the computational cost to 1/100th or 1/1000th of their parent quantum methods, hence they are able to describe the charge transfer process and bond-breaking and forming.
The semi-empirical methodologies are based on a functional Hamiltonian and approximated wavefunction equation, albeit with certain approximations (see below). Minimum basis sets methodologies with parameterized Hamiltonians based on Hartree-Fock have been derived starting with the Huckel model and a number of improvements that applied for light elements. This development has not however been extended to the 5f-elements, and would prove a challenge given the complicated electronic structure of the 4f- and 5f-elements and the drastic simplification implied by the minimum basis assumption.
Density functional tight binding (DFTB) is an attractive approach to achieve a rapid calculation of forces in the same manner as the empirical potentials while retaining the electronic degrees of freedom explicitly, as with DFT. In simple terms, this approach uses a similar formulation to DFT, in the sense that the governing equations are also a diagonalization of a Hamiltonian problem, although in order to speed up the calculation, the Hamiltonian is parameterized for the different types of interactions and as a function of the relative interatomic distances. Hence, matrix elements between two basis functions, which would involve computing the double volume integral, are reduced to a simple arithmetic calculation (function of rij), decreasing the computational cost enormously. Implementations of DFTB have been reported to be as efficient as linear scaling between the computational cost (hours to run the calculation) and the number of particles (atoms or electrons). This could enable large-scale, long-duration simulations required for realistic molecular dynamics simulations of solution environments. These time-saving improvements are encouraging, allowing DFTB to reach thousands of atoms in a realistic MD simulation. Furthermore, because DFTB is quantum mechanical in nature it captures many-body effects, formation of covalent bonds, charge transfer between species of different electronegativities, and spin polarization (open-shell atoms). Hence, it is well suited to the simulation of interactions in liquids.
As highlighted above, the elements of the Hamiltonian matrix are parameterized, that is, written as a function of the interatomic separation vectors. Here lies the main difficulty of making DFTB usable, in the production of such functions that accurately capture the behavior of the Hamiltonian for an arbitrary atomic configuration. We should add that, because the parameterization is for matrix elements, one would expect the development of accurate parameterizations to be easier than parameterizing a whole interaction empirical potential, although this is far from a trivial exercise. A scaling difficulty still remains because the Hamiltonian matrix elements are for pairs of atoms. Therefore, the parameterization of DFTB will correspond to pairs of atom types. For example, H–H, O–O, and O–H parameterizations are required to simulate an aqueous medium, yet, unlike with an empirical potential, these parameters will also be useful if the medium contains OH, O2, H2O2, etc. If one wanted to simulate uranyl ions (UO22+) in water, parameterizations of U–O, U–H, and U–U terms should be added to the previously stated ones. For each new element to be included in a simulation, all the pairs of terms should be parameterized in advance. Without the parameterization for specific atom types, no MD trajectory can be simulated.
Currently, only a few groups around the world are dedicating efforts to developing parameterizations for DFTB, and the accuracy of each set of parameters will depend on how the group developed it. At least one DFTB parameterization currently exists for each element in the periodic table—except for the 5f-elements. Unfortunately, there is a dearth of models available for simulating f-block elements with only two sets of parameters published to date, namely, interactions of Pu–H, developed for solid-state simulations, and the U–O–H system, for aqueous solution chemistry of uranium. These are the first attempts to obtain promising results, but improvement is still needed. Furthermore, parameterizations of interactions with other elements, such as U–C, U–N, U–Cl, etc., and not only uranium but all the 5f-elements are very much needed to study actinide complexes and model chemical processes with the solvents used in the laboratory.
Outlook
Our understanding of the intricacy of actinide systems has come a long way, yet numerous questions remain unresolved. As we progress, it is essential to address the urgent need for methodological advancements to navigate the challenging time and length scales we encounter, ensuring a thorough statistical sampling of phase space.
To be predictive for actinide chemistry across a wide spectrum of chemical systems, we are in serious need to expand the chemical space of the above parameterized methodologies such as DFTB and empirical potentials. This is essential to properly capture charge transfer and chemical reactivity. However, in expanding the parameter space to encompass a wider range of chemical reactions the number of high level (DFT, multi-reference, etc.) calculations will rapidly increase and with it the computer time demanded. To reduce this burden and increase efficiency, we see the incorporation of advanced machine learning techniques, such as active learning, and physics- and chemistry-informed techniques, to be an essential step in the training process.
Furthermore, exploring kinetics simulations beyond sampling is vital as it elucidates reaction pathways for rare, rate-determining events, yet is understudied. A pivotal, but unaddressed question involves determining the influence of particular actinides on both the kinetics and complex reaction networks. For example, variations in f-element configurations across the series may significantly influence reaction outcomes, leading to a diversity of products. Therefore, the role and effects of 5f electrons across the actinide series remain an open question.
Finally, coupling machine learning techniques with methodologies development, as well as with simulation techniques, will enable multi-fidelity and multi-scale simulations. Such approaches appear promising not only to increase the prediction accuracy but also to improve the time and length scales, facilitating more effective simulations of the complex chemistry and materials of actinides.

Ping Yang serves as the Deputy Director of the G.T. Seaborg Institute for Transactinium Science and a Staff Scientist in the Physics and Chemistry of Materials group of the Theoretical Division at LANL. Yang’s research aims to elucidate the fundamental electronic structure and reactivity of actinides complexes, nanoparticles, and surfaces. She holds a keen interest in leveraging high-performance computing frameworks and data science to develop new computational techniques for simulating complex actinide systems over long timescales, and to accelerate f-element separation.

Enrique R. Batista, received a B.S. in physics from the University of Buenos Aires, Argentina, and an M.S. and Ph.D. from the U. of Washington. After a postdoctoral fellowship at Columbia University he joined LANL in 2003 in what is now part of T-1 (Physics and Chemistry of Materials). Batista is the current Deputy Center Director of the Center for Nonlinear Studies (CNLS). His research focuses on development of computational methodology and application to studies of actinide science, gas phase spectroscopy, and solution and surface science chemistry.
